Naive Bayes

</details> </div>

Naive Bayes est une famille de modèles génératifs qui prédit $p(y=c \vert\mathbf{x})$ en supposant que toutes les caractéristiques sont conditionnellement indépendantes étant donné l’étiquette : $x_i \perp x_j \vert y , \forall i,j$. Naive Bayes fait l’hypothèse que toutes les caractéristiques x_i sont conditionnellement indépendantes de $x_j$ étant donné l’étiquette y, pour tous $i,j$. Cette hypothèse de simplification est très rarement vraie en pratique, ce qui rend l’algorithme “naïf”. Classifier avec une telle hypothèse est très simple :

Notez que, comme nous sommes dans un cadre de classification, $y$ prend des valeurs discrètes, donc $p(y=c, \pmb\theta)=\pi_c$ est une distribution catégorielle.

Vous vous demandez peut-être pourquoi nous utilisons l'hypothèse de simplification de l'indépendance conditionnelle. Nous pourrions prédire directement en utilisant $\hat{y} = arg\max_c p(y=c, \pmb\theta)p(\mathbf{x} \vert y=c, \pmb\theta)$. L’hypothèse conditionnelle nous permet d’obtenir de meilleures estimations des paramètres $\pmb{\theta}$ en utilisant moins de données . En effet,$p(\mathbf{x} \vert y=c, \pmb\theta)$ nécessite beaucoup plus de données puisqu’il s’agit d’une distribution de dimension $D$ (pour chaque étiquette possible c), tandis que $\prod_{j=1}^D p(x_j \vert y=c, \pmb\theta)$ la factorise en $D$ distributions unidimensionnelles, nécessitant beaucoup moins de données à ajuster en raison de la malédiction de la dimensionnalité. En plus de nécessiter moins de données, cela permet également de mélanger facilement différentes familles de distributions pour chaque caractéristique.

Nous devons encore répondre à deux questions importantes :

• Quelle famille de distributions utiliser pour $p(x_j \vert y=c, \pmb\theta)$ (souvent appelée modèle d’événement du classificateur Naive Bayes) ?
• Comment estimer les paramètres $\theta$?

Modèles d’événements du Naive Bayes

La famille de distributions à utiliser est un choix de conception important qui donnera lieu à des types spécifiques de classificateurs Naive Bayes. Il est important de noter que la famille de distributions $p(x_j \vert y=c, \pmb\theta)$ n’a pas besoin d’être la même pour tous les $j$, ce qui permet d’utiliser des caractéristiques très différentes (exemple : des données continues et discrètes). En pratique, on utilise souvent la distribution Gaussienne pour les caractéristiques continues, et les distributions Multinomiale ou Bernoulli pour les caractéristiques discrètes :

Naive Bayes Gaussien :

Utiliser une distribution Gaussienne est une hypothèse typique lorsqu’on traite des données continues $x_j \in \mathbb{R}$. Cela revient à supposer que chaque caractéristique, conditionnée par l’étiquette, suit une distribution Gaussienne univariée :

Notez que si toutes les caractéristiques sont supposées gaussiennes, cela correspond à ajuster une distribution Gaussienne multivariée avec une covariance diagonale : $p(\mathbf{x} \vert y=c, \pmb\theta)= \mathcal{N}(\mathbf{x};\pmb\mu_{c},\text{diag}(\pmb\sigma_{c}^2))$.

 La limite de décision est quadratique car elle correspond aux ellipses (gaussiens) qui interceptent .

Naive Bayes Multinomial :

Dans le cas des caractéristiques catégoriques $x_j \in \{1,…, K\}$ on peut utiliser une distribution Multinomiale, où $\theta_{jc}$ représente la probabilité d’avoir la caractéristique $j$ à n’importe quel moment pour un exemple de classe $c$ :

Naive Bayes Multinomial est généralement utilisé pour la classification de documents, et correspond à la représentation de tous les documents sous forme de sac de mots (sans ordre). On estime alors $\theta_{jc}$ en comptant les occurrences des mots pour déterminer les proportions de fois où le mot $j$ apparaît dans un document classé comme $c$.

L’équation ci-dessus est appelée Naive Bayes bien que les caractéristiques $x_j$ ne soient techniquement pas indépendantes en raison de la contrainte $\sum_j x_j = const$. La procédure de formation est toujours la même parce que pour la classification, nous ne nous soucions que de comparer les probabilités plutôt que leurs valeurs absolues, auquel cas Multinomial Naive Bayes donne en fait les mêmes résultats qu'un produit de Categoryical Naive Bayes dont les caractéristiques satisfont la propriété de l'indépendance conditionnelle.

Naive Bayes Multinomial est un classificateur linéaire lorsqu’il est exprimé en espace logarithmique :

Naive Bayes Bernoulli Multivarié :

Dans le cas des caractéristiques binaires $x_j \in \{0,1\}$ on peut utiliser une distribution Bernoulli, où $\theta_{jc}$ représente la probabilité que la caractéristique $j apparaisse dans la classe c$:

Le Naive Bayes Bernoulli est typiquement utilisé pour classer des textes courts, et correspond à l’examen de la présence et de l’absence de mots dans une phrase (sans tenir compte des comptes).

Le Naive Bayes Bernoulli multivarié n’est pas équivalent à l’utilisation du Naive Bayes Multinomial avec des comptes de fréquence tronqués à 1 .En effet, il modélise à la fois l’absence et la présence des mots.

Entraînement

Enfin, nous devons entraîner le modèle en trouvant les meilleurs paramètres estimés $\hat\theta$. Cela peut être fait soit en utilisant des estimations ponctuelles (par exemple MLE), soit avec une perspective bayésienne.

Estimation du Maximum de Vraisemblance (MLE) :

La log-vraisemblance négative du jeu de données $\mathcal{D}=\{\mathbf{x}^{(n)},y^{(n)}\}_{n=1}^N$ est :

Comme la log-vraisemblance négative se décompose en termes qui dépendent uniquement de $\pi$ et de chaque $\theta_{jc}$, nous pouvons optimiser tous les paramètres séparément.

En minimisant le premier terme en utilisant des multiplicateurs de Lagrange pour imposer $\sum_c \pi_c$, , nous obtenons que $\hat\pi_c = \frac{N_c}{N}$. qui est naturellement la proportion d’exemples étiquetés avec $y=c$.

La valeur de $\theta{jc}$ dépend de la famille de distribution que nous utilisons. Dans le cas du Multinomial, on peut montrer que $\hat\theta{jc}=\frac{N_{jc}}{N_c}$. Ce qui est très simple à calculer, car il suffit de compter le nombre de fois qu’une certaine caractéristique $x_j$ est observée dans un exemple avec l’étiquette $y=c$.

Estimation Bayésienne :

Le problème avec l’estimation du maximum de vraisemblance (MLE) est qu’elle conduit souvent à du sur-apprentissage (overfitting). Par exemple, si une caractéristique est toujours présente dans tous les échantillons d’entraînement (par exemple le mot “the” dans la classification de documents), alors le modèle échouera s’il voit un échantillon de test sans cette caractéristique, car il attribuera une probabilité de 0 à toutes les étiquettes.

En adoptant une approche bayésienne, le sur-apprentissage est atténué grâce aux a priori. Pour ce faire, nous devons calculer l’apostériori :

Using (factored) conjugate priors (Dirichlet for Multinomial, Beta for Bernoulli, Gaussian for Gaussian), this gives the same estimates as in the MLE case (the prior has the same form than the likelihood and posterior) but regularized.

The Bayesian framework requires predicting by integrating out all the parameters $\pmb\theta$. The only difference with the first set of equations we have derived for classifying using Naive Bayes, is that the predictive distribution is conditioned on the training data $\mathcal{D}$ instead of the parameters $\pmb\theta$:

Comme auparavant, le terme à maximiser se décompose en un terme par paramètre. Tous les paramètres peuvent donc être maximisés indépendamment. Ces intégrales sont généralement intraitables, mais dans le cas des distributions Gaussienne, Multinomiale et Bernoulli avec leurs a priori conjugués correspondants, nous pouvons heureusement calculer une solution sous forme fermée.

Dans le cas du Multinomial (et du Bernoulli), la solution est équivalente à la prédiction avec une estimation ponctuelle $\hat{\pmb\theta}=\bar{\pmb\theta}$. Où $\bar{\pmb\theta}$ est la moyenne de la distribution postérieure

En utilisant un a priori symétrique de Dirichlet : $p(\pmb\pi)=\text{Dir}(\pmb\pi; \pmb{1}\alpha_\pi)$ , nous obtenons que $\hat\pi_c = \bar\pi_c = \frac{N_c + \alpha_\pi }{N + \alpha_\pi C}$.

Le Naive Bayes bayésien Multinomial est équivalent à prédire avec une estimation ponctuelle :

I.e. C’est-à-dire que le Naive Bayes bayésien Multinomial avec un a priori symétrique de Dirichlet assigne une distribution postérieure prédictive :

Le modèle graphique correspondant est :

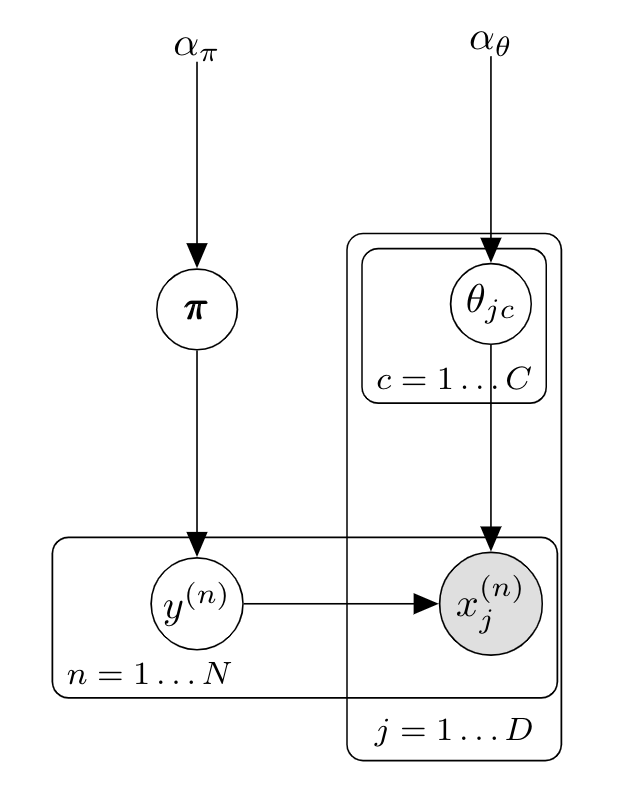
Lorsque l’on utilise un a priori uniforme $\alpha_\theta=1$, cette équation est appelée lissage de Laplace ou lissage additif d’unité. $\alpha$ représente intuitivement un “pseudo-compte” $\alpha_\theta$ pour les caractéristiques $x_{jc}$ . Pour la classification de documents , cela correspond simplement à attribuer un compte initial non nul à tous les mots, ce qui évite le problème de trouver un document de test $x^{(t)}$ with $p(y=c\vert x^{(t)})=0$ s’il contient un seul mot $x_{j}^*$ qui n’a jamais été vu dans un document d’entraînement avec l’étiquette $c$. $\alpha=1$ est un choix commun dans les exemples bien que des valeurs plus petites fonctionnent souvent mieux.

Remarques :

• Le terme “Naive” provient de l’indépendance conditionnelle des caractéristiques étant donné l’étiquette. La partie “Bayes” du nom provient de l’utilisation du théorème de Bayes pour utiliser un modèle génératif, mais il ne s’agit pas d’une méthode bayésienne puisqu’il n’est pas nécessaire de marginaliser sur tous les paramètres.

• Si nous estimions le Naive Bayes Multinomial en utilisant une estimation a posteriori maximale (MAP) au lieu de la MSE ou de la méthode bayésienne, nous prédirions en utilisant le mode de l’apostériori (au lieu de la moyenne dans le cas bayésien) $\hat\theta_{jc}=\frac{N_{jc} + \alpha - 1}{N_c + (\alpha -1)D}$ (de même pour $\pmb\pi$). Cela signifie que le lissage de Laplace peut également être interprété comme l’utilisation de MAP avec un a priori non uniforme $\text{Dir}(\pmb\theta; \pmb{2})$. Mais lorsque l’on utilise un a priori uniforme de Dirichlet, MAP coïncide avec la MSE.

• Le Naive Bayes Gaussien est équivalent à l’analyse discriminante quadratique lorsque chaque matrice de covariance $\Sigma_c$ est diagonale.

• Le Naive Bayes discret et la régression logistique forment une “paire génératif-discriminatif”, car ils prennent tous deux la même forme (linéaire en probabilités logarithmiques) mais estiment les paramètres différemment. Par exemple, dans le cas binaire, Naive Bayes prédit la classe avec la probabilité la plus élevée. C’est-à-dire qu’il prédit $C_1$ si $\log \frac{p(C_1 \vert \pmb{x})}{p(C_2 \vert \pmb{x})} = \log \frac{p(C_1 \vert \pmb{x})}{1-p(C_1 \vert \pmb{x})} > 0$. Nous avons vu que le Naive Bayes discret est linéaire dans l’espace logarithmique, donc nous pouvons réécrire l’équation comme $\log \frac{p(C_1 \vert \pmb{x})}{1-p(C_1 \vert \pmb{x})} = 2 \log p(C_1 \vert \pmb{x}) - 1 = 2 \left( b + \mathbf{w}^T_c \mathbf{x} \right) - 1 = b' + \mathbf{w'}^T_c \mathbf{x} > 0$. Cette régression linéaire sur le ratio de cotes logarithmique correspond exactement à la forme de la régression logistique (l’équation habituelle est récupérée en résolvant $\log \frac{p}{1-p} = b + \mathbf{w'}^T \mathbf{x}$). On peut montrer la même chose pour Naive Bayes Multinomial et la régression logistique multinomiale.

• Pour la classification de documents, il est courant de remplacer les comptes bruts dans le Naive Bayes Multinomial par des poids tf-idf .

Ressources : Voir la section 3.5 du K. Murphy's book pour toutes les étapes de dérivation et les exemples.