Classification
Classification
![]() Compare to : Regression
Compare to : Regression
Decision Trees
Vue d'ensemble
-
 Intuition :
Intuition :- Diviser les données d'entraînement en fonction de "la meilleure" question (par exemple : a-t-il plus de 27 ans ?). Diviser récursivement les données tant que les résultats de classification ne sont pas satisfaisants.
- Les arbres de décision sont essentiellement l'algorithme à utiliser pour le jeu des "20 questions". Akinator est un bon exemple de ce qui peut être mis en œuvre avec des arbres de décision. Akinator est probablement basé sur des systèmes experts de logique floue (car il peut fonctionner avec des réponses incorrectes), mais vous pourriez créer une version plus simple avec des arbres de décision.
- Les divisions "optimales" sont trouvées par maximisation du gain d'information ou par des méthodes similaires.
-
 Pratique :
Pratique :- Les arbres de décision sont très utiles lorsque vous avez besoin d'un modèle simple et interprétable, mais que la relation entre $y$ et $\mathbf{x}$ est complexe.
- Complexité de l'entraînement : $O(MND + ND\log(N) )$ .
- Complexité des tests : $O(MT)$ .
- Notation utilisée : $M=depth$ ; \(N= \#_{train}\) ; \(D= \#_{features}\) ; \(T= \#_{test}\).
-
 Avantages :
Avantages :- Interprétable .
- Peu d'hyperparamètres.
- Nécessite moins de nettoyage des données :
- Pas besoin de normalisation.
- Peut gérer les valeurs manquantes.
- Gère les variables numériques et catégorielles.
- Robuste aux valeurs aberrantes.
- Ne fait pas d'hypothèses sur la distribution des données.
- Effectue une sélection de caractéristiques.
- S'adapte bien à grande échelle.
-
 Inconvénients :
Inconvénients :- Précision généralement faible à cause de la sélection gloutonne.
- Forte variance car si la première division change, tout change.
- Les divisions sont parallèles aux axes des caractéristiques => il faut plusieurs divisions pour séparer deux classes avec une frontière de décision à 45°.
- Pas d'apprentissage en ligne.
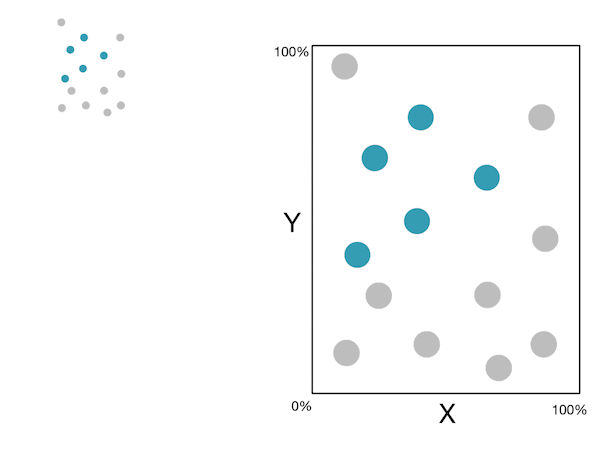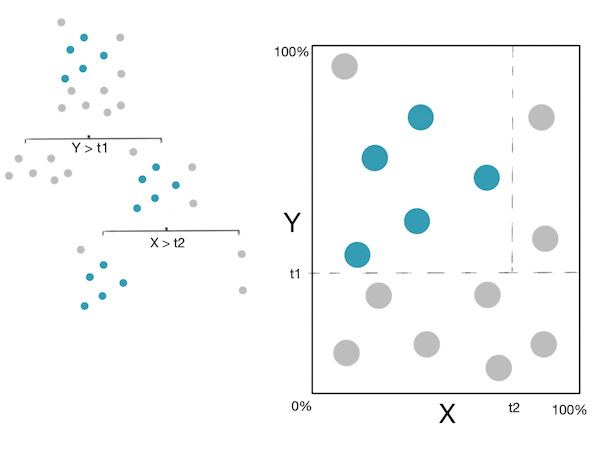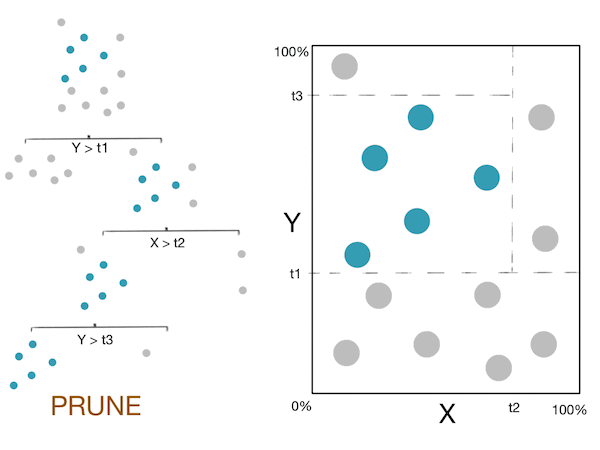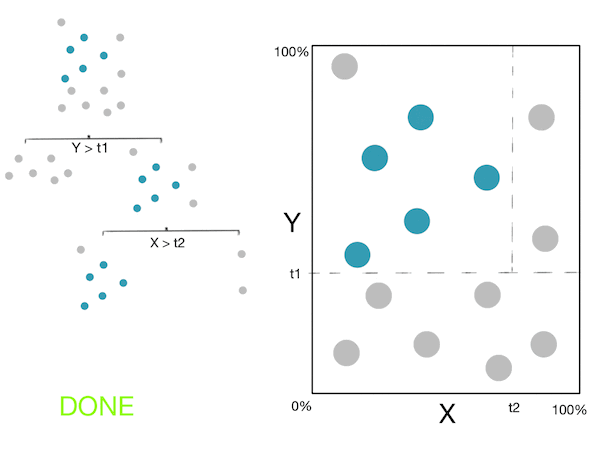
L’idée de base derrière la construction d’un arbre de décision est de :
- Trouver une séparation optimale (caractéristique + seuil). C’est-à-dire la séparation qui minimise l’impureté (maximise le gain d’information).
- Diviser le jeu de données en 2 sous-ensembles basés sur la séparation ci-dessus.
- Appliquer récursivement les étapes $1$ et $2$ à chaque nouveau sous-ensemble jusqu’à ce qu’un critère d’arrêt soit atteint.
- Pour éviter le surapprentissage : élaguer les nœuds qui “ne sont pas très utiles”.
Voici un petit GIF montrant ces étapes :
Note: For more information, please see the "details" and "Pseudocode and Complexity" drop-down below.
Détails
L'idée derrière les arbres de décision est de partitionner l'espace d'entrée en plusieurs régions. Par exemple, la région des hommes de plus de 27 ans. Ensuite, on prédit la classe la plus probable pour chaque région, en attribuant la mode des données d'entraînement dans cette région. Malheureusement, trouver une partition optimale est généralement infaisable sur le plan informatique (NP-complet) en raison du nombre combinatoire élevé d'arbres possibles. En pratique, les différents algorithmes utilisent donc une approche gloutonne. C’est-à-dire que chaque séparation de l’arbre de décision essaie de maximiser un certain critère, indépendamment des séparations suivantes.
Comment définir un critère d’optimalité pour une séparation ? Définissons une impureté (erreur) de l’état actuel que nous allons essayer de minimiser. Voici trois impuretés possibles :
-
Erreur de classification :
-
 L’erreur d’exactitude : $1-Acc$ de l’état actuel. C’est-à-dire l’erreur que nous commettrions en nous arrêtant à l’état actuel.>
L’erreur d’exactitude : $1-Acc$ de l’état actuel. C’est-à-dire l’erreur que nous commettrions en nous arrêtant à l’état actuel.> - \[ClassificationError = 1 - \max_c (p(c))\]
-
-
Entropie:
-
 À quel point les classes de l’état actuel sont-elles imprévisibles.
À quel point les classes de l’état actuel sont-elles imprévisibles.
- Minimiser l’entropie correspond à maximiser le gain d’information.
- \[Entropie = - \sum_{c=1}^C p(c) \log_2 \ p(c)\]
-
-
Impureté de Gini :
-
 Probabilité attendue ($\mathbb{E}[\cdot] = \sum_{c=1}^C p(c) (\cdot) de mal classer un élément sélectionné au hasard, s’il était classé selon la distribution des étiquettes$) ($\sum_{c=1}^C p(c) (1-p(c))$) .
Probabilité attendue ($\mathbb{E}[\cdot] = \sum_{c=1}^C p(c) (\cdot) de mal classer un élément sélectionné au hasard, s’il était classé selon la distribution des étiquettes$) ($\sum_{c=1}^C p(c) (1-p(c))$) . - \[ClassificationError = \sum_c^C p_c (1-p_c) = 1- \sum_c^C p_c^2\]
-
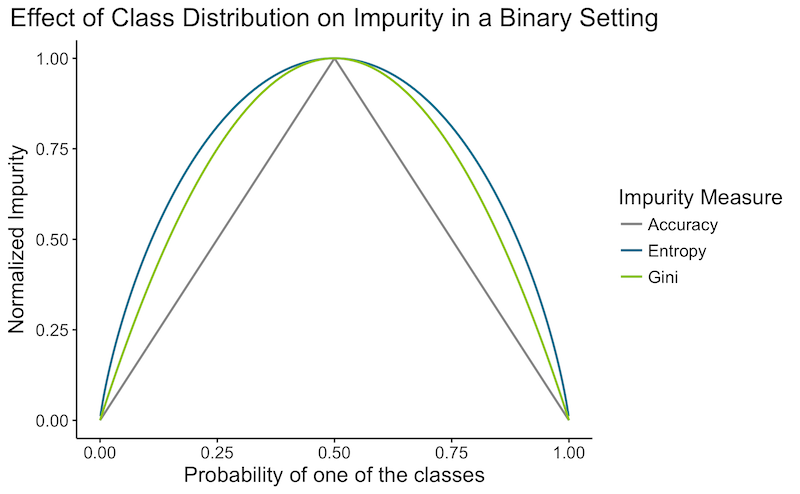
Voici un graphique rapide montrant l'impureté en fonction d'une distribution de classe dans un paramètre binaire :
![]() Notes supplémentaires : :
Notes supplémentaires : :
- L’erreur de classification peut sembler être un choix naturel, mais ne vous laissez pas tromper par les apparences : elle est généralement moins performante que les deux autres méthodes :
- Elle est “plus” gloutonne que les autres. En effet, elle ne se concentre que sur l’erreur actuelle, tandis que l’impureté de Gini et l’entropie tentent de créer une séparation plus pure, ce qui facilitera les étapes suivantes. Supposons que nous ayons une classification binaire avec 100 observations dans chaque classe $(100,100)$. Comparons une séparation qui divise les données en $(20,80)$ et $(80,20)$ à une autre qui les divise en $(40,100)$ et $(60,0)$. Dans les deux cas, l’erreur de précision serait de 0,20 %. Mais nous préférerions le deuxième cas, qui est pur et n’aura pas besoin d’être divisé davantage. L’impureté de Gini et l’entropie choisiraient correctement cette dernière.
- L’erreur de classification ne prend en compte que la classe la plus probable. Ainsi, une séparation avec deux classes extrêmement probables aura une erreur similaire à celle d’une séparation avec une classe extrêmement probable et plusieurs classes improbables.
- L’impureté de Gini et l’entropie diffèrent dans moins de 2 % des cas, comme vous pouvez le voir dans le graphique ci-dessus. L’entropie est légèrement plus lente à calculer en raison de l’opération logarithmique.
Quand devons-nous arrêter de diviser ? Il est important de ne pas diviser trop souvent afin d’éviter le surapprentissage. Voici quelques heuristiques pouvant être utilisées comme critères d’arrêt :
- Lorsque le nombre d’exemples d’entraînement dans un nœud feuille est faible.
- Lorsque la profondeur atteint un seuil.
- Lorsque l’impureté est faible.
- Lorsque le gain de pureté dû à la séparation est faible.
De telles heuristiques nécessitent des seuils dépendants du problème (hyperparamètres) et peuvent donner des résultats relativement mauvais. Par exemple, les arbres de décision peuvent être amenés à diviser les données sans aucun gain de pureté, afin d’atteindre des gains de pureté élevés à l’étape suivante. Il est donc courant de construire de grands arbres en utilisant le nombre d’exemples d’entraînement dans un nœud feuille comme critère d’arrêt. Pour éviter le surapprentissage, l’algorithme élaguera ensuite l’arbre résultant. Dans l’algorithme CART, le critère d’élagage $C_{pruning}(T)$ équilibre l’impureté et la complexité du modèle grâce à une régularisation. La variable régularisée est souvent le nombre de nœuds feuilles $\vert T \vert$, comme illustré ci-dessous :
\[C_{pruning}(T) = \sum^{\vert T \vert }_{v=1} I(T,v) + \lambda \vert T \vert\]$\lambda$ est sélectionné via la validation croisée et permet de faire un compromis entre l’impureté et la complexité du modèle, pour un arbre donné $T$, avec des nœuds feuilles $v=1…\vertT \vert$ en utilisant la mesure d’impureté $I$.
Variantes : il existe différentes méthodes d’arbres de décision, qui diffèrent selon les points suivants :
- Critère de séparation ? Gini / Entropie.
- Technique pour réduire le surapprentissage ?
- Combien de variables peuvent être utilisées dans une séparation ?
- Construction d’arbres binaires ?
- Gestion des valeurs manquantes ?
- Gèrent-ils la régression ?
- Robustesse face aux valeurs aberrantes ?
Variantes célèbres :
ID3 : première implémentation d’arbre de décision. Non utilisé en pratique.
C4.5 : Amélioration de ID3 par le même développeur. Élagage basé sur l’erreur. Utilise l’entropie. Gère les valeurs manquantes. Sensible aux valeurs aberrantes. Peut créer des branches vides.
CART : Utilise Gini. Élagage basé sur la complexité des coûts. Arbres binaires. Gère les valeurs manquantes. Gère la régression. Pas sensible aux valeurs aberrantes.
CHAID : Trouve une variable de séparation en utilisant le test du Khi-carré pour tester la dépendance entre une variable et une réponse. Pas d’élagage. Semble meilleur pour décrire les données, mais moins performant pour la prédiction.
D’autres variantes incluent : C5.0 (prochaine version de C4.5, probablement moins utilisée car elle est brevetée), MARS.
![]() Resources Une étude comparative de différentes méthodes d'arbre de décision.
Resources Une étude comparative de différentes méthodes d'arbre de décision.
Pseudocode et complexité
-
Pséudocode
La version simple d'un arbre de décision peut être écrite en quelques lignes de pseudocode python :
def buildTree(X,Y):
if stop_criteria(X,Y) :
# if stop then store the majority class
tree.class = mode(X)
return Null
minImpurity = infinity
bestSplit = None
for j in features:
for T in thresholds:
if impurity(X,Y,j,T) < minImpurity:
bestSplit = (j,T)
minImpurity = impurity(X,Y,j,T)
X_left,Y_Left,X_right,Y_right = split(X,Y,bestSplit)
tree.split = bestSplit # adds current split
tree.left = buildTree(X_left,Y_Left) # adds subsequent left splits
tree.right buildTree(X_right,Y_right) # adds subsequent right splits
return tree
def singlePredictTree(tree,xi):
if tree.class is not Null:
return tree.class
j,T = tree.split
if xi[j] >= T:
return singlePredictTree(tree.right,xi)
else:
return singlePredictTree(tree.left,xi)
def allPredictTree(tree,Xt):
t,d = Xt.shape
Yt = vector(d)
for i in t:
Yt[i] = singlePredictTree(tree,Xt[i,:])
return Yt
- Complexité J’utiliserai la notation suivante : \(M=depth\) ; \(K=\#_{thresholds}\) ; \(N = \#_{train}\) ; \(D = \#_{features}\) ; \(T = \#_{test}\) .
Réfléchissons d’abord à la complexité de construction de la première souche de décision (premier appel de fonction) :
- Dans une souche de décision, nous parcourons toutes les caractéristiques et tous les seuils $O(KD)$, , puis calculons l’impureté. L’impureté dépend uniquement des probabilités de classes. Calculer les probabilités signifie parcourir toutes les données $X$ et compter les $Y$ : $O(N)$. Avec ce pseudocode simple, la complexité temporelle pour construire une souche est donc $O(KDN)$.
- En réalité, il n’est pas nécessaire de tester des seuils arbitraires, seulement les valeurs uniques prises par au moins un exemple. Par exemple, il n’est pas nécessaire de tester $feature_j>0.11$ et $feature_j>0.12$ lorsque tous les $feature_j$ sont soit $0.10$ or $0.80$. Remplaçons le nombre de seuils possibles $K$ par la taille du jeu d’entraînement $N$. La complexité devient. $O(N^2D)$
- Actuellement, nous parcourons deux fois toutes les données $X$, une fois pour les seuils et une fois pour calculer l’impureté. Si les données étaient triées par la caractéristique actuelle, l’impureté pourrait simplement être mise à jour au fur et à mesure que nous parcourons les exemples. Par exemple, lorsque nous considérons la règle $feature_j>0.8$après avoir déjà considéré $feature_j>0.7$, nous n’avons pas besoin de recalculer toutes les probabilités de classes : nous pouvons simplement prendre les probabilités de $feature_j>0.7$ et faire les ajustements en sachant le nombre d’exemples avec $feature_j==0.7$. Pour chaque caractéristique $j$, nous devrions d’abord trier toutes les données $O(N\log(N))$ , puis parcourir une fois en $O(N)$, ce qui donnerait finalement $O(DN\log(N))$.
Nous avons maintenant la complexité d’une souche de décision. Vous pourriez penser que trouver la complexité de la construction d’un arbre reviendrait à la multiplier par le nombre d’appels de fonction, n’est-ce pas ? Pas vraiment, ce serait une surestimation. En effet, à chaque appel de fonction, la taille des données d’entraînement $N$ aurait diminué. L’intuition derrière le résultat que nous recherchons est qu’à chaque niveau $l=1…M$ la somme des données d’entraînement dans chaque fonction reste $N$. Plusieurs fonctions travaillant en parallèle avec un sous-ensemble d’exemples prennent le même temps qu’une seule fonction avec l’ensemble d’entraînement complet $N$. La complexité à chaque niveau reste donc $O(DN\log(N))$ , ce qui fait que la complexité pour construire un arbre de profondeur $M$ est $O(MDN\log(N))$. Voici une preuve que le travail à chaque niveau reste constant :
À chaque itération, le jeu de données est divisé en $\nu$ sous-ensembles de $k_i$ éléments et un ensemble de $n-\sum_{i=1}^{\nu} k_i$. Chaque niveau, le coût total serait donc (en utilisant les propriétés des logarithmes et le fait que $k_i \le N$ ) :
\[\begin{align*} cost &= O(k_1D\log(k_1)) + ... + O((N-\sum_{i=1}^{\nu} k_i)D\log(N-\sum_{i=1}^{\nu} k_i))\\ &\le O(k_1D\log(N)) + ... + O((N-\sum_{i=1}^{\nu} k_i)D\log(N))\\ &= O(((N-\sum_{i=1}^{\nu} k_i)+\sum_{i=1}^{\nu} k_i)D\log(N)) \\ &= O(ND\log(N)) \end{align*}\]Le dernier ajustement possible que je vois est de tout trier une fois, de stocker les données et simplement d’utiliser ces données pré-calculées à chaque niveau. La complexité finale de l’entraînement est donc $O(MDN + ND\log(N))$ .
La complexité temporelle pour faire des prédictions est simple : pour chaque t exemples, il faut parcourir une question à chaque niveau $M$. C’est-à-dire $O(MT)$ .
Naive Bayes
Vue d'ensemble
-
 Intuition :
Intuition :- Dans le cas discret : "comptage anticipé". *Par exemple * Étant donné une phrase $x_i$ à classer comme spam ou non, comptez toutes les fois où chaque mot $w^i_j$ était dans une phrase de spam précédemment vue et prédis comme spam si le total (pondéré) "nombre de spam" est supérieur au nombre de "nombre de spam non spam".
- Utilisez une hypothèse d'indépendance conditionnelle ("naive") pour avoir de meilleures estimations des paramètres même avec peu de données.
-
 Pratique :
Pratique :- Bonne et simple référence de base.
- Performant lorsque le nombre de caractéristiques est grand mais que la taille du jeu de données est faible.
- Complexité de l'entraînement : $O(ND)$ .
- Complexité du test : $O(TDK)$ .
- Notation utilisée : \(N= \#_{train}\) ; \(K= \#_{classes}\) ; \(D= \#_{features}\) ; \(T= \#_{test}\).
-
 Avantages :
Avantages :- Simple à comprendre et à implémenter.
- Rapide et scalable (entraînement et test).
- Gère l'apprentissage en ligne.
- Fonctionne bien avec peu de données.
- Pas sensible aux caractéristiques non pertinentes.
- Gère les données réelles et discrètes.
- Probabiliste.
- Gère les valeurs manquantes.
-
 Inconvénients :
Inconvénients :- Hypothèse forte d'indépendance conditionnelle des caractéristiques étant donné les étiquettes.
- Sensible aux caractéristiques rarement observées (atténué par lissage).
Naive Bayes est une famille de modèles génératifs qui prédit $p(y=c \vert\mathbf{x})$ en supposant que toutes les caractéristiques sont conditionnellement indépendantes, étant donné l’étiquette : $x_i \perp x_j \vert y , \forall i,j$. Il s’agit d’une hypothèse simplificatrice qui est très rarement vraie en pratique, ce qui rend l’algorithme “naïf”. Classifier avec une telle hypothèse est très simple :
\[\begin{aligned} \hat{y} &= arg\max_c p(y=c\vert\mathbf{x}, \pmb\theta) \\ &= arg\max_c \frac{p(y=c, \pmb\theta)p(\mathbf{x}\vert y=c, \pmb\theta) }{p(x, \pmb\theta)} & & \text{Règle de Bayes} \\ &= arg\max_c \frac{p(y=c, \pmb\theta)\prod_{j=1}^D p(x_\vert y=c, \pmb\theta) }{p(x, \pmb\theta)} & & \text{Assumption conditionnelle de l'indépendance} \\ &= arg\max_c p(y=c, \pmb\theta)\prod_{j=1}^D p(x_j\vert y=c, \pmb\theta) & & \text{Dénominateur constant} \end{aligned}\]Notez que, puisque nous sommes dans un cadre de classification, $y$ prend des valeurs discrètes, donc $p(y=c, \pmb\theta)=\pi_c$ est une distribution catégorielle.
Vous vous demandez peut-être pourquoi nous utilisons l’hypothèse simplificatrice d’indépendance conditionnelle. Nous pourrions directement prédire en utilisant $\hat{y} = arg\max_c p(y=c, \pmb\theta)p(\mathbf{x} \vert y=c, \pmb\theta)$. L’hypothèse d’indépendance conditionnelle nous permet d’avoir de meilleures estimations des paramètres $\theta$ en utilisant moins de données . En effet, $p(\mathbf{x} \vert y=c, \pmb\theta)$ nécessite beaucoup plus de données car il s’agit d’une distribution en $D$ dimensions (pour chaque étiquette possible $c$), tandis que $\prod_{j=1}^D p(x_j \vert y=c, \pmb\theta)$ la factorise en $D$ 1-distributions unidimensionnelles, ce qui nécessite beaucoup moins de données en raison de la malédiction de la dimensionnalité. En plus de nécessiter moins de données, cela permet également de facilement combiner différentes familles de distributions pour chaque caractéristique.
Nous devons encore aborder deux questions importantes :
- Quelle famille de distributions utiliser pour $p(x_j \vert y=c, \pmb\theta)$ (souvent appelée le modèle d’événements du classificateur Naive Bayes) ?
- Comment estimer les paramètres $\theta$?
Modèles d’événements de Naive Bayes
La famille de distributions à utiliser est un choix de conception important qui donnera lieu à des types spécifiques de classificateurs Naive Bayes. Il est important de noter que la famille de distributions $p(x_j \vert y=c, \pmb\theta)$ n’a pas besoin d’être la même pour tous les $j$, ce qui permet d’utiliser des caractéristiques très différentes (par exemple des données continues et discrètes). En pratique, on utilise souvent la distribution gaussienne pour les caractéristiques continues, et les distributions multinomiale ou de Bernoulli pour les caractéristiques discrètes :
Gaussian Naive Bayes :
L’utilisation d’une distribution gaussienne est une hypothèse typique lorsqu’on traite des données continues $x_j \in \mathbb{R}$. L’utilisation d’une distribution gaussienne est une hypothèse typique lorsqu’on traite des données continues.
\[p(x_j \vert y=c, \pmb\theta) = \mathcal{N}(x_j;\mu_{jc},\sigma_{jc}^2)\]Notez que si toutes les caractéristiques sont supposées gaussiennes, cela correspond à ajuster une gaussienne multivariée avec une matrice de covariance diagonale : $p(\mathbf{x} \vert y=c, \pmb\theta)= \mathcal{N}(\mathbf{x};\pmb\mu_{c},\text{diag}(\pmb\sigma_{c}^2))$.
La frontière de décision est quadratique car elle correspond à des ellipses (gaussiennes) qui se croisent . .
Multinomial Naive Bayes :
Dans le cas des caractéristiques catégorielles $x_j \in \{1,…, K\}$ nous pouvons utiliser une distribution multinomiale, où $\theta_{jc}$ désigne la probabilité d’avoir la caractéristique $j$à n’importe quelle étape d’un exemple de classe $c$ :
\[p(\pmb{x} \vert y=c, \pmb\theta) = \operatorname{Mu}(\pmb{x}; \theta_{jc}) = \frac{(\sum_j x_j)!}{\prod_j x_j !} \prod_{j=1}^D \theta_{jc}^{x_j}\]Naive Bayes multinomial est typiquement utilisé pour la classification de documents , et correspond à représenter tous les documents comme un sac de mots (sans ordre). Nous estimons ensuite (voir ci-dessous) $\theta_{jc}$ en comptant les occurrences des mots pour trouver les proportions de fois où le mot $j$ est trouvé dans un document classé comme $c$.
L’équation ci-dessus est appelée Naive Bayes bien que les caractéristiques $x_j$ ne soient techniquement pas indépendantes en raison de la contrainte $\sum_j x_j = const$. La procédure d’entraînement reste cependant la même car, pour la classification, nous nous soucions uniquement de comparer les probabilités plutôt que de leurs valeurs absolues. Dans ce cas, Naive Bayes multinomial donne en fait les mêmes résultats qu’un produit de Naive Bayes catégoriel dont les caractéristiques respectent la propriété d’indépendance conditionnelle.
Naive Bayes multinomial est un classificateur linéaire lorsqu’il est exprimé dans l’espace logarithmique :
\[\begin{aligned} \log p(y=c \vert \mathbf{x}, \pmb\theta) &\propto \log \left( p(y=c, \pmb\theta)\prod_{j=1}^D p(x_j \vert y=c, \pmb\theta) \right)\\ &= \log p(y=c, \pmb\theta) + \sum_{j=1}^D x_j \log \theta_{jc} \\ &= b + \mathbf{w}^T_c \mathbf{x} \\ \end{aligned}\]Naive Bayes Bernoulli multivarié :
Dans le cas des caractéristiques binaires $x_j \in \{0,1\}$ nous pouvons utiliser une distribution de Bernoulli, où $\theta_{jc}$ représente la probabilité que la caractéristique $j$ se manifeste dans la classe $c$:
\[p(x_j \vert y=c, \pmb\theta) = \operatorname{Ber}(x_j; \theta_{jc}) = \theta_{jc}^{x_j} \cdot (1-\theta_{jc})^{1-x_j}\]Naive Bayes Bernoulli est typiquement utilisé pour classifier des textes courts , et correspond à l’observation de la présence ou de l’absence de mots dans une phrase (sans compter les occurrences).
Naive Bayes Bernoulli multivarié n’est pas identique à l’utilisation de Naive Bayes multinomial avec les fréquences d’occurrence tronquées à 1. En effet, il modélise l’absence des mots en plus de leur présence.
Entraînement
Enfin, nous devons entraîner le modèle en trouvant les meilleurs paramètres estimés $\hat\theta$. Cela peut être fait soit en utilisant des estimations ponctuelles (par exemple MLE), soit avec une approche bayésienne.
Estimation du Maximum de Vraisemblance (MLE) :
La log-vraisemblance négative du jeu de données $\mathcal{D}=\{\mathbf{x}^{(n)},y^{(n)}\}_{n=1}^N$ est :
\[\begin{aligned} NL\mathcal{L}(\pmb{\theta} \vert \mathcal{D}) &= - \log \mathcal{L}(\pmb{\theta} \vert \mathcal{D}) \\ &= - \log \prod_{n=1}^N \mathcal{L}(\pmb{\theta} \vert \mathbf{x}^{(n)},y^{(n)}) & & \textit{i.i.d} \text{ dataset} \\ &= - \log \prod_{n=1}^N p(\mathbf{x}^{(n)},y^{(n)} \vert \pmb{\theta}) \\ &= - \log \prod_{n=1}^N \left( p(y^{(n)} \vert \pmb{\pi}) \prod_{j=1}^D p(x_{j}^{(n)} \vert\pmb{\theta}_j) \right) \\ &= - \log \prod_{n=1}^N \left( \prod_{c=1}^C \pi_c^{\mathcal{I}[y^{(n)}=c]} \prod_{j=1}^D \prod_{c=1}^C p(x_{j}^{(n)} \vert \theta_{jc})^{\mathcal{I}[y^{(n)}=c]} \right) \\ &= - \log \left( \prod_{c=1}^C \pi_c^{N_c} \prod_{j=1}^D \prod_{c=1}^C \prod_{n : y^{(n)}=c} p(x_{j}^{(n)} \vert \theta_{jc}) \right) \\ &= - \sum_{c=1}^C N_c \log \pi_c + \sum_{j=1}^D \sum_{c=1}^C \sum_{n : y^{(n)}=c} \log p(x_{j}^{(n)} \vert \theta_{jc}) \\ \end{aligned}\]Comme la log-vraisemblance négative se décompose en termes qui dépendent uniquement de $\pi$ et de chaque $\theta_{jc}$ nous pouvons optimiser tous les paramètres séparément.
En minimisant le premier terme en utilisant des multiplicateurs de Lagrange pour imposer $\sum_c \pi_c$,, nous obtenons que $\hat\pi_c = \frac{N_c}{N}$. ce qui correspond naturellement à la proportion d’exemples étiquetés avec $y=c$.
La valeur de $\theta_{jc}$ dépend de la famille de distribution que nous utilisons. Dans le cas du modèle multinomial, il peut être démontré que $\hat\theta_{jc}=\frac{N_{jc}}{N_c}$. Cela est très facile à calculer, car il suffit de compter le nombre de fois où une certaine caractéristique $x_j$ est observée dans un exemple avec l’étiquette $y=c$.
Estimation Bayésienne :
Le problème avec l’estimation du maximum de vraisemblance (MLE) est qu’elle conduit à du surapprentissage. Par exemple, si une caractéristique est toujours présente dans tous les échantillons d’entraînement (par exemple le mot “the” dans la classification de documents), le modèle échouera s’il rencontre un échantillon de test sans cette caractéristique, car il attribuerait une probabilité de 0 à toutes les étiquettes.
En adoptant une approche bayésienne, le surapprentissage est atténué grâce à l’utilisation de priors (a priori). Pour ce faire, il est nécessaire de calculer la probabilité a posteriori : \(\begin{aligned} p(\pmb\theta \vert \mathcal{D}) &= \prod_{n=1}^N p(\pmb\theta \vert \mathbf{x}^{(n)},y^{(n)}) & \textit{i.i.d} \text{ dataset} \\ &\propto \prod_{n=1}^N p(\mathbf{x}^{(n)},y^{(n)} \vert \pmb\theta)p(\pmb\theta) \\ &\propto \prod_{c=1}^C \left( \pi_c^{N_c} \cdot p(\pi_c) \right) \prod_{j=1}^D \prod_{c=1}^C \prod_{n : y^{(n)}=c} \left( p(x_{j}^{(n)} \vert \theta_{jc}) \cdot p(\theta_{jc}) \right) \\ \end{aligned}\)
En utilisant des priors conjugués (facteurs) (Dirichlet pour le Multinomial, Beta pour le Bernoulli, Gaussienne pour le Gaussien), cela donne les mêmes estimations que dans le cas de l’estimation du maximum de vraisemblance (MLE) (le prior a la même forme que la vraisemblance et la probabilité a posteriori), mais avec régularisation.
Le cadre bayésien nécessite de prédire en intégrant tous les paramètres $\pmb\theta$. La seule différence avec le premier ensemble d’équations que nous avons dérivé pour la classification en utilisant Naive Bayes, est que la distribution prédictive est conditionnée par les données d’entraînement $\mathcal{D}$ au lieu des paramètres $\pmb\theta$: \(\begin{aligned} \hat{y} &= arg\max_c p(y=c \vert \pmb{x},\mathcal{D}) \\ &= arg\max_c \int p(y=c\vert \pmb{x},\pmb\theta) p(\pmb\theta \vert \mathcal{D}) d\pmb\theta\\ &= arg\max_c \int p(\pmb\theta\vert\mathcal{D}) p(y=c \vert\pmb\theta) \prod_{j=1}^D p(x_j\vert y=c, \pmb\theta) d\pmb\theta \\ &= arg\max_c \left( \int p(y=c\vert\pmb\pi) p(\pmb\pi \vert \mathcal{D}) d\pmb\pi \right) \prod_{j=1}^D \int p(x_j\vert y=c, \theta_{jc}) p(\theta_{jc}\vert\mathcal{D}) d\theta_{jc} & & \text{Factored prior} \\ \end{aligned}\)
Comme précédemment, le terme à maximiser se décompose en un terme par paramètre. Tous les paramètres peuvent donc être maximisés indépendamment. Ces intégrales sont généralement intraitables, mais dans le cas de la Gaussienne, du Multinomial et du Bernoulli avec leurs priors conjugués correspondants, nous pouvons heureusement calculer une solution sous forme fermée.
Dans le cas du Multinomial (et du Bernoulli), la solution équivaut à prédire avec une estimation ponctuelle $\hat{\pmb\theta}=\bar{\pmb\theta}$. Où $\bar{\pmb\theta}$ est la moyenne de la distribution a posteriori.
En utilisant un prior Dirichlet symétrique : $p(\pmb\pi)=\text{Dir}(\pmb\pi; \pmb{1}\alpha\pi)$ nous obtenons que $\hat\pi_c = \bar\pi_c = \frac{N_c + \alpha\pi }{N + \alpha_\pi C}$.
Le Naive Bayes Multinomial bayésien équivaut à prédire avec une estimation ponctuelle :
\[\bar\theta_{jc} = \hat\theta_{jc}=\frac{N_{jc} + \alpha }{N_c + \alpha D}\]I.e. Naive Bayes Multinomial Bayésien avec un prior Dirichlet symétrique attribue une distribution a posteriori prédictive :
\[p(y=c\vert\mathbf{x},\mathcal{D}) \propto \frac{N_c + \alpha_\theta }{N + \alpha_\theta C} \prod_{j=1}^D \frac{N_{jc} + \alpha_\theta }{N_c + \alpha_\theta D}\]Le modèle graphique correspondant est :
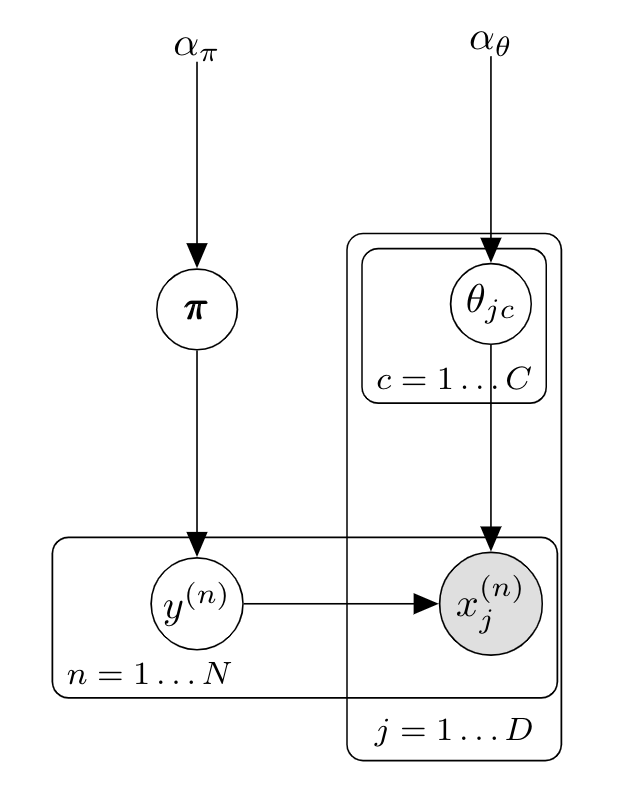
Lorsqu’on utilise un prior uniforme $\alpha_\theta=1$,cette équation est appelée lissage de Laplace ou lissage additif. Intuitivement, $\alpha$ représente un “pseudo-comptage” $\alpha_\theta$ des caractéristiques $x_{jc}$ . Pour la classification de documents , cela correspond simplement à attribuer un comptage initial non nul à tous les mots, ce qui évite le problème d’avoir un document de test $x^{(t)}$ avec $p(y=c\vert x^{(t)})=0$ s’il contient un seul mot $x_{j}^*$ qui n’a jamais été vu dans un document d’entraînement avec l’étiquette $c$. $\alpha=1$ est un choix courant dans les exemples, bien que des valeurs plus petites fonctionnent souvent mieux . .
![]() Notes supplémentaires :
Notes supplémentaires :
Le terme “Naïf” vient de l’indépendance conditionnelle des caractéristiques étant donné l’étiquette. La partie “Bayes” du nom vient de l’utilisation du théorème de Bayes pour utiliser un modèle génératif, mais ce n’est pas une méthode bayésienne car elle ne nécessite pas de marginaliser sur tous les paramètres.
Si nous estimions le Naive Bayes multinomial en utilisant l’estimation du maximum a posteriori (MAP) au lieu de la MSE ou de la méthode bayésienne, nous prédirions en utilisant la mode de la distribution a posteriori (au lieu de la moyenne dans le cas bayésien) : $\hat\theta_{jc}=\frac{N_{jc} + \alpha - 1}{N_c + (\alpha -1)D}$ (de même pour $\pmb\pi$). Cela signifie que le lissage de Laplace pourrait également être interprété comme utilisant MAP avec un prior non uniforme $\text{Dir}(\pmb\theta; \pmb{2})$. Mais lorsque l’on utilise un prior Dirichlet uniforme, MAP coïncide avec la MSE.
Le Naive Bayes gaussien est équivalent à l’analyse discriminante quadratique lorsque chaque matrice de covariance $\Sigma_c$ est diagonale.
Naive Bayes discrète et la régression logistique forment un “couple génératif-discriminatif”, car ils prennent la même forme (linéaire dans les probabilités logarithmiques) mais estiment les paramètres différemment. Par exemple, dans le cas binaire, Naive Bayes prédit la classe avec la plus grande probabilité. C’est-à-dire qu’il prédit $C_1$ si $\log \frac{p(C_1 \vert \pmb{x})}{p(C_2 \vert \pmb{x})} = \log \frac{p(C_1 \vert \pmb{x})}{1-p(C_1 \vert \pmb{x})} > 0$. Nous avons vu que Naive Bayes discrète est linéaire dans l’espace logarithmique, donc nous pouvons réécrire l’équation comme $\log \frac{p(C_1 \vert \pmb{x})}{1-p(C_1 \vert \pmb{x})} = 2 \log p(C_1 \vert \pmb{x}) - 1 = 2 \left( b + \mathbf{w}^T_c \mathbf{x} \right) - 1 = b' + \mathbf{w'}^T_c \mathbf{x} > 0$. Cette régression linéaire sur le ratio de cotes logarithmiques est exactement la forme de la régression logistique (l’équation habituelle est retrouvée en résolvant $\log \frac{p}{1-p} = b + \mathbf{w'}^T \mathbf{x}$). La même chose peut être démontrée pour Naive Bayes multinomial et la régression logistique multinomiale.
Pour la classification de documents, il est courant de remplacer les comptages bruts dans Naive Bayes multinomial par des poids tf-idf.
![]() Ressources : Voir la section 3.5 du livre de K. Murphy pour tous les détails de la dérivation et des exemples.
Ressources : Voir la section 3.5 du livre de K. Murphy pour tous les détails de la dérivation et des exemples.
Regression
Arbres de décision
Les arbres de décision sont plus souvent utilisés pour les problèmes de classification.
Les deux différences avec les arbres de décision pour la classification sont :
- Quelle erreur minimiser pour une séparation optimale ? Cela remplace la mesure d’impureté dans le cadre de la classification. Une fonction d’erreur largement utilisée pour la régression est la somme des erreurs au carré. Nous n’utilisons pas l’erreur quadratique moyenne afin que la soustraction de l’erreur avant et après une séparation ait du sens. La somme des erreurs au carré pour la région $R$ est :
- Que prédire pour une région donnée ? Dans le cadre de la classification, nous prédisions la mode du sous-ensemble des données d’entraînement dans cette région. Prendre la mode n’a pas de sens pour une variable continue. Maintenant que nous avons défini une fonction d’erreur ci-dessus, nous voudrions prédire une valeur qui minimise cette somme des erreurs au carré. Cela correspond à la valeur moyenne de la région. Prédire la moyenne est intuitivement ce que nous aurions fait.
Jetons un coup d’œil à un graphique simple pour mieux comprendre l’algorithme :
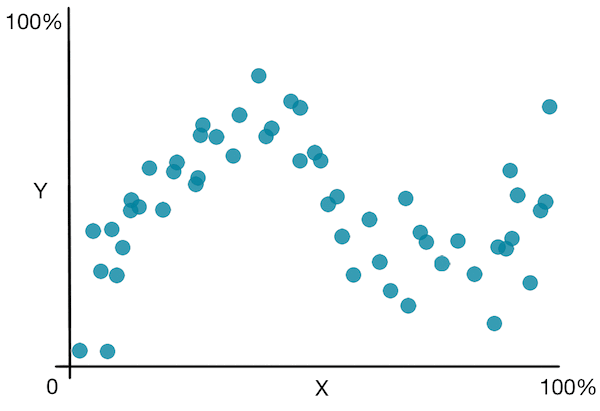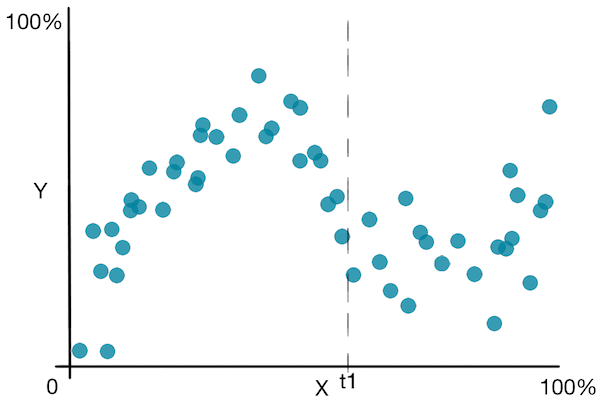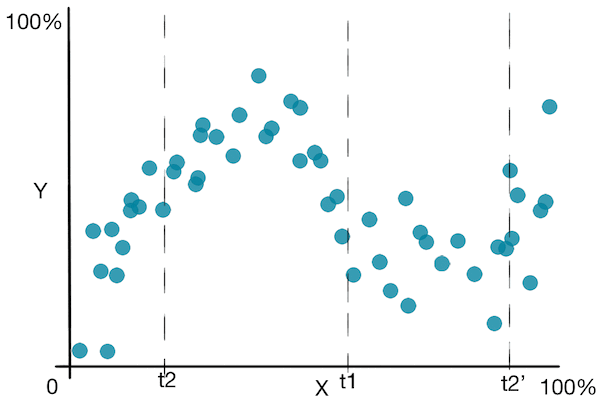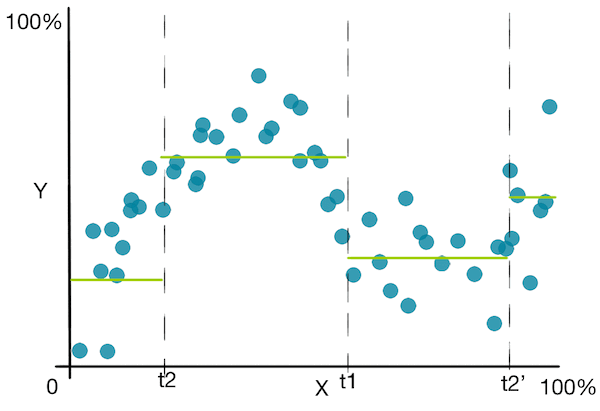
![]() En plus des inconvénients vus dans les arbres de décision pour la classification, les arbres de décision pour la régression souffrent du fait qu’ils prédisent une fonction non lisse .
En plus des inconvénients vus dans les arbres de décision pour la classification, les arbres de décision pour la régression souffrent du fait qu’ils prédisent une fonction non lisse .