Métriques d'évaluation

Métriques de Classification

Métriques simples

Notes secondaires : L'accent est mis sur la classification binaire, mais la plupart des scores peuvent être généralisés au paramètre multi-classes. Souvent, cela est réalisé en considérant uniquement la "classe correcte" et la "classe incorrecte" afin d'en faire une classification binaire, puis vous faites la moyenne (pondérée par la proportion d'observation dans la classe) le score de chaque classe.

• TP / TN / FN / FP: Mieux compris à travers un \(2*2\) confusion matrix.

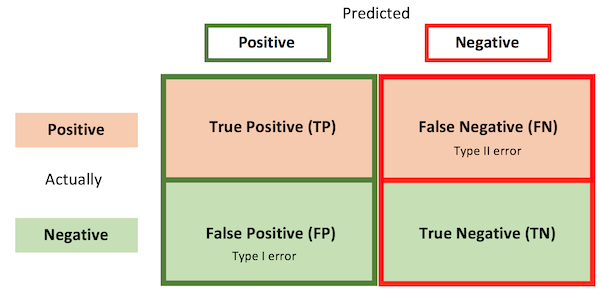
• Exactitude (Accuracy) : Fraction des observations correctement classées.

  • $Acc = \frac{Vrais Positifs}{Total} = \frac{TP+FN}{TP+FN+TN+FP}$

  • 💡 Intuition : En général, à quel point peut-on faire confiance aux prédictions ?

  • 🔧 Pratique : À utiliser si aucune classe n’est déséquilibrée et si le coût des erreurs est le même pour les deux types.

• Précision (Precision) : Fraction des prédictions positives qui étaient effectivement positives.

  • $Precision = \frac{TP}{Prédictions Positives} = \frac{TP}{TP+FP}$

  • 💡 Intuition : À quel point peut-on faire confiance aux prédictions positives ?

  • 🔧 Pratique : À utiliser si les faux positifs (FP) sont les pires erreurs.

• Rappel (Recall) : Fraction des observations positives qui ont été correctement prédites.
  • $ Rappel = \frac{TP}{Observations Positives} = \frac{TP}{TP+FN}$
  • 💡 Intuition : Combien de vrais positifs allons-nous trouver ?
  • 🔧 Pratique : À utiliser si les faux négatifs (FN) sont les pires erreurs.

• F1-Score : Moyenne harmonique (utile pour la moyenne des taux) du rappel et de la précision.

  • $F1 = 2 \frac{Précision * Rappel}{Précision + Rappel}$
    • Si le rappel est $\beta$ fois plus important que la précision, utilisez : $F_{\beta} = (1 + \beta^2) \frac{Précision* Rappel}{\beta^2 Précision + Rappel}$

  • 💡 Intuition : À quel point pouvons-nous faire confiance à nos algorithmes pour la classe positive ?

  • 🔧 Pratique : À utiliser si la classe positive est la plus importante (par exemple, lorsque l’on cherche un détecteur plutôt qu’un classificateur).
• Spécificité (Specificity) : Rappel pour les classes négatives.
  • $ Spécificité = \frac{TN}{Observations Négatives} = \frac{TN}{TN+FP}$

• Log-Loss : Mesure la performance lorsque le modèle produit une probabilité $\hat{y_{ic}}$ que l’observation n appartienne à la classe c.

  • Aussi appelée perte d’entropie croisée ou perte logistique.

  • $ LogLoss = - \frac{1}{N} \sum_{n=1}^N \sum_{c=1}^C y_{nc} \ln(\hat{y}_{nc})$

  • Utilisez le logarithme naturel pour la cohérence.

  • Intègre l’idée de confiance probabiliste.

  • La Log-Loss est la métrique minimisée par la régression logistique et plus généralement par le Softmax.

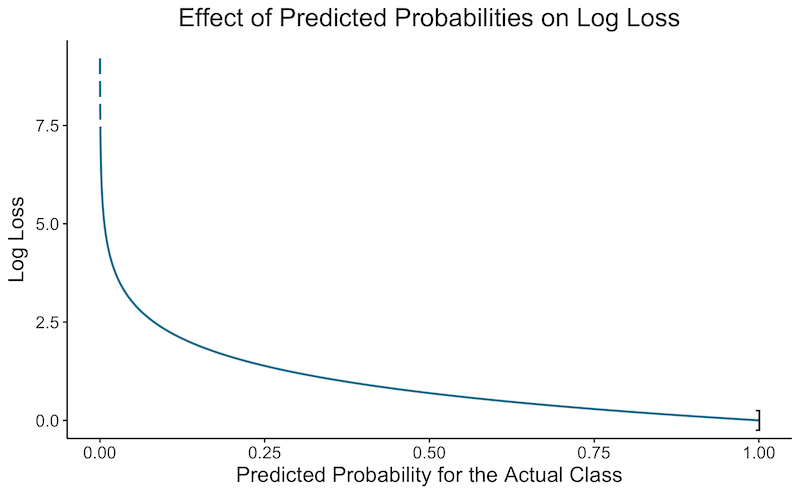
  • 💡 Intuition : Pénalise davantage si le modèle est confiant mais se trompe (voir graphique ci-dessous).

  • 💡 Log-loss est l’entropie croisée entre la distribution des vraies étiquettes et les prédictions.

  • 🔧 Pratique : À utiliser lorsque vous vous intéressez à la confiance dans les résultats.

  • Le graphique ci-dessous montre la log-loss en fonction de la confiance de l’algorithme pour classer une observation dans la bonne catégorie. Pour plusieurs observations, on calcule la log-loss de chacune, puis on en fait la moyenne.

• Kappa de Cohen : Amélioration de votre classificateur comparée à la simple supposition de la classe la plus probable.

  • $\kappa = \frac{exactitude - \%{ClasseMax}}{1 - \%{ClasseMax}}$

  • Souvent utilisée pour calculer la fiabilité inter-évaluateurs (ex : 2 humains) : $\kappa = \frac{p_o- p_e}{1 - p_e}$ où $p_o$ est l’accord observé et $p_e$ est l’accord attendu par hasard.

  • $ \kappa \leq 1$ (si $<0$ , le résultat est inutile).

  • 💡 Intuition : Amélioration de l’exactitude pondérée par le déséquilibre des classes.

  • 🔧 Pratique : À utiliser lorsque le déséquilibre entre les classes est important et que toutes les classes sont d’importance similaire.

• AUC (Area Under the Curve) : Résume les courbes en une seule métrique.

  • Elle fait généralement référence à la courbe ROC, mais peut aussi être utilisée pour d’autres courbes comme celle précision-rappel.
  • 💡 Intuition : Probabilité qu’une observation positive sélectionnée aléatoirement soit prédite avec un score plus élevé qu’une observation négative sélectionnée aléatoirement.
    • 💡 AUC évalue les résultats à tous les points de coupure possibles. Cela permet d’obtenir de meilleures informations sur la capacité du classificateur à séparer les classes. Cela la rend très différente des autres métriques qui dépendent généralement d’un seuil de coupure (par exemple, 0,5 pour la régression logistique).
  • 🔧 Pratique : À utiliser lors de la création d’un classificateur pour des utilisateurs ayant des besoins différents (ils pourraient ajuster le point de coupure). De mon expérience, l’AUC est largement utilisée en statistique (~métrique de référence en biostatistiques), mais moins en machine learning.
    • Prédictions aléatoires : $AUC = 0.5$. Prédictions parfaites : $AUC = 1$.

Métriques visuelles

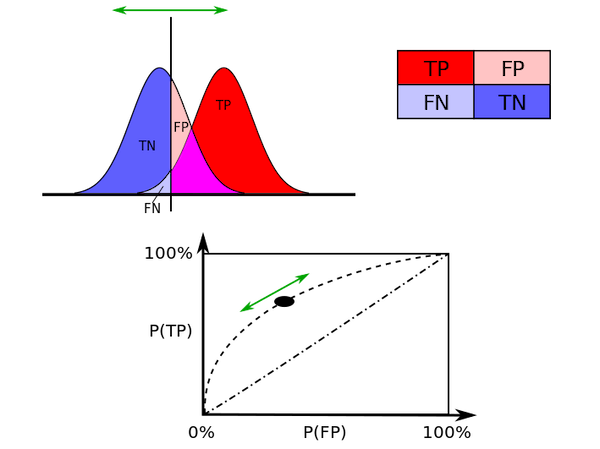
• Courbe ROC : Receiver Operating Characteristic
• Graphique montrant le taux de vrais positifs (TP) par rapport au taux de faux positifs (FP), sur un seuil variable.
• Ce graphique de Wikipédia l’illustre bien :

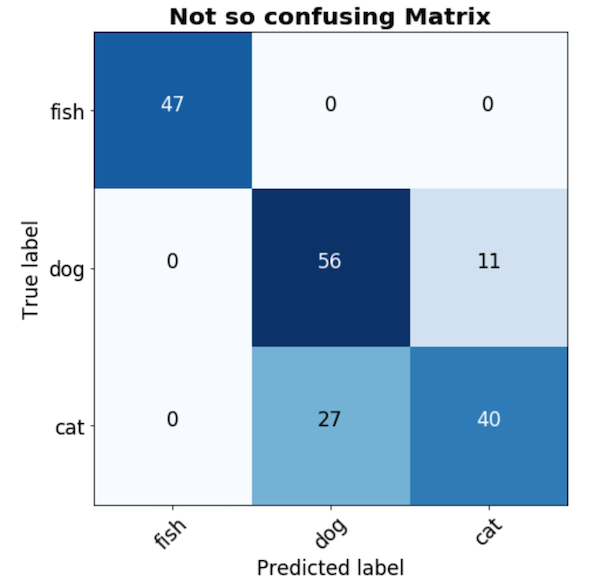
• Matrice de confusion : Une matrice $C*C$ qui montre le nombre d’observations de la classe $c$ ayant été étiquetées $c', \ \forall c=1 \ldots C \text{ et } c'=1\ldots C$.

  • ​Remarque : Faites attention, les gens ne sont pas toujours cohérents avec les axes : vous pouvez trouver des matrices “réel-prédit” et “prévu-réel”.

  • Cela est mieux compris avec un exemple :