Concepts de Machine Learning

\[H(X) = H(p) \equiv \mathbb{E}\left[\operatorname{I} (p_i)\right] = \sum_{i=1}^K p_i \ \log(\frac{1}{p_i}) = - \sum_{i=1}^K p_i\ \log(p_i)\]

Intuition :

• L'entropie d'une variable aléatoire est l'information attendue. C'est-à-dire la quantité de surprise attendue en observant une variable aléatoire .
• L'entropie représente le nombre attendu de bits (en supposant $log_2$) nécessaires pour coder une observation d'une variable aléatoire (discrète) selon le schéma de codage optimal .

Notes annexes :

• $H(X) \geq 0$

• L'entropie est maximisée lorsque tous les événements se produisent avec une probabilité uniforme. Si $X$ peut prendre $n$ valeurs alors : $max(H) = H(X_{uniform})= \sum_i^K \frac{1}{K} \log(\frac{1}{ 1/K} ) = \log(K)$

  </div>

</details>

Explication Complète

Le concept d'entropie est central à la fois en thermodynamique et en théorie de l'information, ce que je trouve assez fascinant. À l'origine, il provient de la thermodynamique statistique et est si important qu'il est gravé sur la tombe de Ludwig Boltzmann (l'un des pères de ce domaine). Vous entendrez souvent :

• Thermodynamique : L'entropie est une mesure du désordre
• Théorie de l'Information : L'entropie est une mesure de l'information

Ces deux façons de penser peuvent sembler différentes, mais en réalité, elles sont exactement les mêmes. Elles répondent essentiellement à la question : à quel point est-il difficile de décrire cette chose ?

Je vais ici me concentrer sur le point de vue de la théorie de l'information, car son interprétation est plus intuitive pour le machine learning. Je ne souhaite pas non plus passer trop de temps à réfléchir à la thermodynamique, car les personnes qui le font se suicident souvent .

\[H(X) = H(p) \equiv \mathbb{E}\left[\operatorname{I} (p_i)\right] = \sum_{i=1}^K p_i \ \log(\frac{1}{p_i}) = - \sum_{i=1}^K p_i\ \log(p_i)\]

En théorie de l'information, il existe deux façons intuitives de penser à l'entropie. Elles sont mieux expliquées par un exemple :

Supposons que mon ami Claude me propose d'aller voir un match de NBA (Cavaliers contre Spurs) ce soir. Malheureusement, je ne peux pas venir, mais je lui demande de noter qui marque chaque panier. Claude est très geek et utilise un téléphone binaire qui ne peut écrire que des 0 et des 1. Comme il n'a pas beaucoup de mémoire disponible, il veut utiliser le plus petit nombre possible de bits.

1. D'après les matchs précédents, Claude sait que LeBron James marquera très probablement plus souvent que le vieux (mais génial ) Manu Ginobili. Utilisera-t-il le même nombre de bits pour indiquer que LeBron a marqué, que pour Ginobili ? Bien sûr que non, il allouera moins de bits pour les paniers de LeBron puisqu'il les notera plus souvent. Il exploite essentiellement sa connaissance de la distribution des paniers pour réduire le nombre moyen de bits nécessaires pour les noter. Il se trouve que s'il connaissait la probabilité $p_i$ de chaque joueur $i$ de marquer, il devrait encoder leur nom avec $nBit(p_i)=\log_2(1/p_i)$ bits. Cela a été intuitivement construit par Claude (Shannon) lui-même, car c'est la seule mesure (à une constante près) qui satisfait les axiomes de la mesure d'information. L'intuition derrière cela est la suivante :
   • Multiplier les probabilités de 2 joueurs marquant devrait entraîner l'addition de leurs bits. Imaginez que LeBron et Ginobili aient respectivement 0.25 et 0.0625 de probabilité de marquer le prochain panier. Alors, la probabilité que LeBron marque les 2 prochains paniers serait la même que celle de Ginobili marquant un seul panier ($p(LeBron) * p(LeBron) = 0.25 * 0.25 = 0.0625 = Ginobili$). Nous devrions donc allouer 2 fois moins de bits pour LeBron, de sorte qu'en moyenne, nous ajoutons toujours le même nombre de bits par observation. $nBit(LeBron) = \frac{1}{2} * nBit(Ginobili) = \frac{1}{2} * nBit(p(LeBron)^2)$. Le logarithme est une fonction qui transforme les multiplications en sommes, comme requis. Le nombre de bits devrait donc être de la forme $nBit(p_i) = \alpha * \log(p_i) + \beta $
   • Les joueurs ayant une probabilité plus élevée de marquer devraient être encodés avec un nombre de bits inférieur . C'est-à-dire que $nBit$ devrait diminuer lorsque $p_i$ augmente : $nBit(p_i) = - \alpha * \log(p_i) + \beta, \alpha > 0 $
   • Si LeBron avait une probabilité de $100%$ de marquer, pourquoi aurais-je demandé à Claude d'écrire quoi que ce soit ? Je saurais tout a priori . C'est-à-dire que $nBit$ devrait être $0$ pour $p_i = 1$ : $nBit(p_i) = \alpha * \log(p_i), \alpha > 0 $
2. Maintenant, Claude m'envoie le message contenant des informations sur qui a marqué chaque panier. Voir que LeBron a marqué me surprendra moins que Ginobili. Autrement dit, le message de Claude me donne plus d'information lorsqu'il me dit que Ginobili a marqué. Si je voulais quantifier ma surprise pour chaque panier, je devrais créer une mesure qui satisfait les conditions suivantes :
   • Plus la probabilité d'un joueur de marquer est faible, plus je serai surpris . La mesure de surprise devrait donc être une fonction décroissante de la probabilité : $surprise(x_i) = -f(p_i) * \alpha, \alpha > 0$.
   • En supposant que les joueurs marquant soient indépendants les uns des autres, il est raisonnable de demander que ma surprise de voir LeBron et Ginobili marquer à la suite soit la même que la somme de ma surprise de voir LeBron marquer et de voir Ginobili marquer. Autrement dit Multiplier les probabilités indépendantes devrait additionner la surprise : $surprise(p_i * x_j) = surprise(p_i) + surprise(p_j)$.
   • Enfin, la mesure devrait être continue étant donné les probabilités . $surprise(p_i) = -\log(p_{i}) * \alpha, \alpha > 0$

En prenant $\alpha = 1 $ pour simplifier, nous obtenons $surprise(p_i) = -\log(p_i) = nBit(p_i)$. Nous avons ainsi dérivé une formule pour calculer la surprise associée à l'événement $x_i$ et le nombre optimal de bits à utiliser pour encoder cet événement. Cette valeur est appelée contenu d'information $I(p_i)$. Pour obtenir la surprise moyenne / nombre de bits associés à une variable aléatoire $X$, il suffit de prendre l'espérance de tous les événements possibles (c'est-à-dire la moyenne pondérée par la probabilité de l'événement). Cela nous donne la formule de l'entropie $H(X) = \sum_i p_i \ \log(\frac{1}{p_i}) = - \sum_i p_i\ \log(p_i)$

À partir de l'exemple ci-dessus, nous voyons que l'entropie correspond à :

• au nombre attendu de bits pour encoder de manière optimale un message
• à la quantité moyenne d'information obtenue en observant une variable aléatoire

Notes annexes :

• D'après notre dérivation, nous voyons que la fonction est définie à une constante près $\alpha$. C'est la raison pour laquelle la formule fonctionne également bien pour toute base logarithmique, en effet changer de base équivaut à multiplier par une constante. Dans le contexte de la théorie de l'information, nous utilisons $\log_2$.
• L'entropie est la raison (deuxième loi de la thermodynamique) pour laquelle mettre un glaçon dans votre Moscow Mule (mon cocktail favori) ne rend normalement pas votre glaçon plus froid et votre cocktail plus chaud. Je dis "normalement" parce que c'est possible mais très improbable : réfléchissez-y la prochaine fois que vous sirotez votre boisson préférée !

Ressources : Excellente explication du lien entre l'entropie en thermodynamique et en théorie de l'information, [introduction amicale aux

Entropie Différentielle

L'entropie différentielle (= entropie continue) est la généralisation de l'entropie pour les variables aléatoires continues.

Étant donné une variable aléatoire continue $X$ avec une fonction de densité de probabilité $f(x)$ :

\[h(X) = h(f) := - \int_{-\infty}^{\infty} f(x) \log {f(x)} \ dx\]

Si vous deviez deviner, quelle distribution maximise l'entropie pour une variance donnée ? Vous avez deviné : c'est la distribution gaussienne.

Notes annexes : L'entropie différentielle peut être négative.

Entropie Croisée

Nous avons vu que l'entropie est le nombre attendu de bits utilisés pour encoder une observation de $X$ sous le schéma de codage optimal. En revanche, l'entropie croisée est le nombre attendu de bits pour encoder une observation de $X$ sous un schéma de codage incorrect. Appelons $q$ la mauvaise distribution de probabilité utilisée pour créer un schéma de codage. Nous utiliserons alors $- \log(q_i)$ bits pour encoder la $i^{ème}$ valeur possible de $X$. Bien que nous utilisions $q$ comme une distribution de probabilité incorrecte, les observations seront toujours distribuées selon $p$. Nous devons donc prendre la valeur d'espérance sur $p$ :

\[H(p,q) = \mathbb{E}_p\left[\operatorname{I} (q_i)\right] = - \sum_i p_i \log(q_i)\]

De cette interprétation, il s'ensuit naturellement que :

• $H(p,q) > H(p), \forall q \neq p$
• $H(p,p) = H(p)$

Notes annexes : La log loss est souvent appelée perte d'entropie croisée, en effet, elle correspond à l'entropie croisée entre la distribution des vraies étiquettes et les prédictions.

Divergence de Kullback-Leibler

La divergence de Kullback-Leibler (= entropie relative = gain d'information) de $q$ vers $p$ est simplement la différence entre l'entropie croisée et l'entropie :

\[\begin{align*} D_{KL}(p\|q) &= H(p,q) - H(p) \\ &= [- \sum_i p_i \log(q_i)] - [- \sum_i p_i \log(p_i)] \\ &= \sum_i p_i \log\left(\frac{p_i}{q_i}\right) \end{align*}\]

Intuition

• La divergence KL correspond au nombre de bits supplémentaires que vous devrez utiliser en utilisant un schéma de codage basé sur la mauvaise distribution de probabilité $q$ par rapport à la vraie $p$.
• La divergence KL indique en moyenne combien vous serez plus surpris en lançant un dé truqué en pensant qu'il est équitable, par rapport à la surprise de savoir qu'il est truqué.
• La divergence KL est souvent appelée le gain d'information obtenu en utilisant $p$ au lieu de $q$.
• La divergence KL peut être vue comme la "distance" entre deux distributions de probabilité. Mathématiquement, ce n'est pas une distance car elle n'est pas symétrique. Il est donc plus correct de dire qu'il s'agit d'une mesure de la divergence d'une distribution de probabilité $q$ par rapport à une autre $p$.

La divergence KL est souvent utilisée avec les distributions de probabilité des variables aléatoires continues. Dans ce cas, l'espérance implique des intégrales :

\[D_{KL}(p \parallel q) = \int_{- \infty}^{\infty} p(x) \log\left(\frac{p(x)}{q(x)}\right) dx\]

Pour comprendre pourquoi la divergence KL n'est pas symétrique, il est utile de penser à un simple exemple de dé et de pièce (on indiquera pile et face par 0 et 1 respectivement). Les deux sont équitables et donc leur PDF est uniforme. Leur entropie est trivialement : $H(p_{coin})=\log(2)$ et $H(p_{dice})=\log(6)$. Considérons d'abord $D_{KL}(p_{coin} \parallel p_{dice})$. Les 2 événements possibles de $X_{dice}$ sont 0,1, ce qui est aussi possible pour la pièce. Le nombre moyen de bits pour encoder une observation de pièce sous le codage du dé sera donc simplement $\log(6)$, et la divergence KL est de $\log(6)-\log(2)$ bits supplémentaires. Maintenant, considérons le problème dans l'autre sens : $D_{KL}(p_{dice} \parallel p_{coin})$. Nous utiliserons $\log(2)=1$ bit pour encoder les événements de 0 et 1. Mais combien de bits utiliserons-nous pour encoder 3,4,5,6 ? Eh bien, le codage optimal pour le dé n'a pas de codage pour ceux-ci car ils ne se produiront jamais dans son monde. La divergence KL n'est donc pas définie (division par 0). La divergence KL n'est donc pas symétrique et ne peut pas être une distance.

Notes annexes : Minimiser l'entropie croisée par rapport à $q$ revient à minimiser $D_{KL}(p \parallel q)$. En effet, les deux équations sont équivalentes à une constante additive près (l'entropie de $p$) qui ne dépend pas de $q$.

Information Mutuelle

\[\begin{align*} \operatorname{I} (X;Y) = \operatorname{I} (Y;X) &:= D_\text{KL}\left(p(x, y) \parallel p(x)p(y)\right) \\ &= \sum_{y \in \mathcal Y} \sum_{x \in \mathcal X} { p(x,y) \log{ \left(\frac{p(x,y)}{p(x)\,p(y)} \right) }} \end{align*}\]

Intuition : L'information mutuelle entre deux variables aléatoires X et Y mesure combien (en moyenne) d'informations sur l'une des v.a. vous recevez en connaissant la valeur de l'autre. Si $X,\ Y$ sont indépendants, alors connaître $X$ ne donne aucune information sur $Y$, donc $\operatorname{I} (X;Y)=0$ car $p(x,y)=p(x)p(y)$. La quantité maximale d'informations que vous pouvez obtenir sur $Y$ à partir de $X$ est toute l'information de $Y$, i.e. $H(Y)$. C'est le cas pour $X=Y$ : $\operatorname{I} (Y;Y)= \sum_{y \in \mathcal Y} p(y) \log{ \left(\frac{p(y)}{p(y)\,p(y)} \right) = H(Y) }$

Note annexe :

• L'information mutuelle est plus proche du concept d'entropie que du contenu de l'information. En effet, ce dernier n'était défini que pour un résultat d'une variable aléatoire, tandis que l'entropie et l'information mutuelle sont définies pour une v.a. en prenant une espérance.
• $\operatorname{I} (X;Y) \in [0, \min(\operatorname{I} (X), \operatorname{I} (Y;Y))]$
• $\operatorname{I} (X;X) = \operatorname{I} (X)$
• $\operatorname{I} (X;Y) = 0 \iff X \,\bot\, Y$
• La généralisation de l'information mutuelle à $V$ variables aléatoires $X_1,X_2,\ldots,X_V$ est la Corrélation Totale: $C(X_1, X_2, \ldots, X_V) := \operatorname{D_{KL}}\left[ p(X_1, \dots, X_V) \parallel p(X_1)p(X_2)\dots p(X_V)\right]$. Elle représente la quantité totale d'information partagée entre l'ensemble des variables aléatoires. Le minimum $C_\min=0$ lorsque les v.a. ne sont pas statistiquement dépendantes. La corrélation totale maximale se produit lorsqu'une seule v.a. détermine toutes les autres : $C_\max = \sum_{i=1}^V H(X_i)-\max\limits_{X_i}H(X_i)$.
• Inégalité du Traitement de l'Information : pour toute chaîne de Markov $X \rightarrow Y \rightarrow Z$: $\operatorname{I} (X;Y) \geq \operatorname{I} (X;Z)$
• Invariance de Reparamétrisation : pour des fonctions inversibles $\phi,\psi$: $\operatorname{I} (X;Y) = \operatorname{I} (\phi(X);\psi(Y))$

Machine Learning et Entropie

Tout cela est intéressant, mais pourquoi parlons-nous de concepts de théorie de l'information en apprentissage automatique ? Eh bien, il s'avère que de nombreux algorithmes de ML peuvent être interprétés à l'aide de concepts liés à l'entropie.

Les 3 principales manières dont l'entropie apparaît en apprentissage automatique sont les suivantes :

• Maximiser le gain d'information (c'est-à-dire l'entropie) à chaque étape de notre algorithme. Exemple :

  • Lors de la construction des arbres de décision, vous choisissez de manière gloutonne de diviser sur l'attribut qui maximise le gain d'information (c'est-à-dire la différence d'entropie avant et après la division). Intuitivement, vous voulez connaître la valeur de l'attribut qui réduit le plus l'aléa dans vos données.

• Minimiser la divergence KL entre la distribution de probabilité réelle inconnue des observations $p$ et celle prédite $q$. Exemple :

  • L'estimateur du Maximum de Vraisemblance (MLE) de nos paramètres $\hat{ \theta }_{MLE}$ correspond aussi aux paramètres qui minimisent la divergence KL entre notre distribution prédite $q_\theta$ et celle réelle inconnue $p$ (ou l'entropie croisée). C'est-à-dire

\[\hat{ \theta }_{MLE} = \operatorname{argmin}_{ \theta } \, NLL= \operatorname{argmin}_{ \theta } \, D_{KL}(p \parallel q_\theta ) = \operatorname{argmin}_{ \theta } \, H(p,q_\theta )\]

• Minimiser la divergence KL entre $p$ calculatoirement intraitable et une approximation plus simple $q$. En effet, l'apprentissage automatique ne concerne pas seulement la théorie mais aussi la mise en œuvre pratique.Exemple :

  • C'est tout l'objectif de l'Inférence Variationnelle (= variational Bayes) qui approxime les probabilités a posteriori des variables non observées souvent intraitables en raison de l'intégrale dans le dénominateur, transformant ainsi le problème d'inférence en un problème d'optimisation. Ces méthodes sont une alternative aux méthodes d'échantillonnage de Monte Carlo pour l'inférence (e.g. Échantillonnage de Gibbs). En général, les méthodes d'échantillonnage sont plus lentes mais asymptotiquement exactes.

Théorème du No Free Lunch

Aucun modèle ne fonctionne de manière optimale pour chaque problème.

Essayons de prédire le prochain fruit dans la séquence :

Vous diriez probablement :pomme:, non ? Peut-être avec une probabilité plus faible, diriez-vous :mandarine:. Mais avez-vous pensé à dire :pastèque: ? J'en doute. Je ne vous ai jamais dit que la séquence était contrainte dans le type de fruit, mais naturellement, nous faisons l'hypothèse que les données "se comportent bien". Le point ici est que sans connaissance ou hypothèses sur les données, toutes les données futures sont également probables.

Le théorème se base sur cela et affirme que tous les algorithmes ont les mêmes performances lorsqu'on les moyenne sur toutes les distributions de données. Ainsi, la performance moyenne d'un classificateur d'apprentissage profond est la même que celle des classificateurs aléatoires.

Notes annexes :

• Vous entendrez souvent parler de ce théorème lorsqu'on pose une question commençant par "quel est le meilleur […] ?".
• Dans le monde réel, les choses ont tendance à "bien se comporter". Elles sont par exemple souvent (localement) continues. Dans de tels contextes, certains algorithmes sont définitivement meilleurs que d'autres.
• Depuis la publication du théorème en 1996, d'autres méthodes ont conservé la métaphore du déjeuner. Par exemple : les algorithmes kitchen sink, random kitchen sink, fastfood, à la carte, et c'est l'une des raisons pour lesquelles j'ai décidé d'utiliser des exemples de fruits dans ce blog .
• Le théorème a été étendu aux algorithmes d'optimisation et de recherche.

Ressources : La preuve de D. Wolpert.

Paramétrique vs Non Paramétrique

Ces deux types de méthodes se distinguent en fonction de leur réponse à la question suivante : "Utiliserai-je la même quantité de mémoire pour stocker le modèle entraîné sur $100$ exemples que pour stocker un modèle entraîné sur $10 000$ d'entre eux ?" Si oui, alors vous utilisez un modèle paramétrique. Sinon, vous utilisez un modèle non paramétrique.

• Paramétrique :
  • La mémoire utilisée pour stocker un modèle entraîné sur $100$ observations est la même que pour un modèle entraîné sur $10 000$ d'entre elles .
  • C'est-à-dire : Le nombre de paramètres est fixe.
  • Moins coûteux en termes de calcul pour le stockage et la prédiction.
  • Moins de variance.
  • Plus de biais.
  • Fait plus d'hypothèses sur les données pour ajuster moins de paramètres.
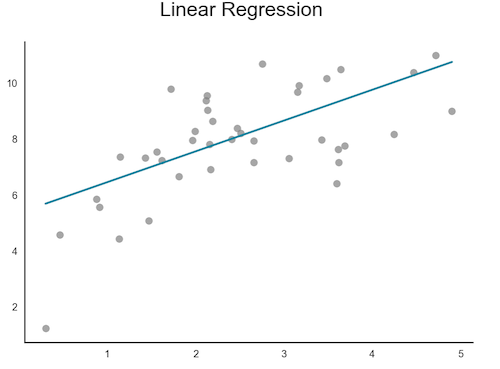
  • Exemple : Clustering K-Means, Régression Linéaire, Réseaux de Neurones :

  

• Non Paramétrique :
  • J'utiliserai moins de mémoire pour stocker un modèle entraîné sur $100$ observations que pour un modèle entraîné sur $10 000$ d'entre elles .
  • C'est-à-dire : Le nombre de paramètres croît avec le jeu d'entraînement.
  • Plus flexible / général.
  • Fait moins d'hypothèses.
  • Moins de biais.
  • Plus de variance.
  • Mauvais si le jeu de test est relativement différent du jeu d'entraînement.
  • Plus coûteux en termes de calcul car il doit stocker et traiter un plus grand nombre de "paramètres" (non borné).
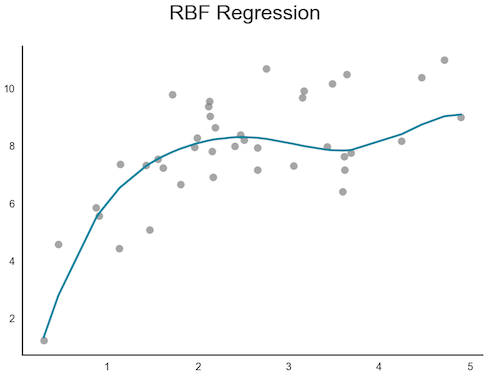
  • Exemple : Clustering K-Plus Proches Voisins, Régression RBF, Processus Gaussiens :

  

Pratique : Commencez avec un modèle paramétrique. Il vaut souvent la peine d'essayer un modèle non paramétrique si : vous faites du clustering, ou si les données d'entraînement sont peu nombreuses mais que le problème est très difficile.

Note annexe : Strictement parlant, tout modèle non paramétrique pourrait être considéré comme un modèle à paramètres infinis. Donc, si vous voulez être pointilleux : la prochaine fois que vous entendez un collègue parler de modèles non paramétriques, dites-lui que c'est en fait paramétrique. Je décline toute responsabilité quant aux conséquences sur votre relation avec lui/elle .